dirk
Comparing star ratings - the Bayesian way
Imagine you want to go to a restaurant and you see the following two ratings
- 5.0 (n = 5)
- 4.8 (n = 500)
How certain can you be that restaurant 1 is the better restaurant?
One complication is that you don’t know the actual distribution of stars for restaurant 2, for the first it is obvious.
We will generate a distribution for restaurant 2 which gives us the actual mean of 4.8.
array([ 10, 10, 10, 10, 460])
We will use the Multinomial-Dirichlet model to estimate the posterior distribution given a prior and the data. The Dirichlet gives us a vector that adds to 1.
Our Dirichlet prior will be the following given we know that many people give 1, 4, or 5 stars.
alpha = [.25, .125, .125, .25, .25]
We use the same prior for both restaurants. We are using pymc as our Bayesian engine.
with pm.Model() as model:
a1 = pm.Dirichlet('a1', alpha)
a2 = pm.Dirichlet('a2', alpha)
# likelihood
y1 = pm.Multinomial('y1', n=5, p=a1, observed=data1)
y2 = pm.Multinomial('y2', n=500, p=a2, observed=data2)
trace = pm.sample()
The model output is the following, you can see that we have 87% probability of 5 stars for R1 and 92% probability of 5 stars for R2.
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
a1[0] 0.041 0.077 0.000 0.182 0.002 0.001 896.0 610.0 1.0
a1[1] 0.020 0.052 0.000 0.104 0.001 0.001 944.0 555.0 1.0
a1[2] 0.020 0.055 0.000 0.102 0.001 0.001 569.0 636.0 1.0
a1[3] 0.041 0.074 0.000 0.180 0.002 0.001 999.0 774.0 1.0
a1[4] 0.877 0.123 0.656 1.000 0.003 0.002 1802.0 1343.0 1.0
a2[0] 0.021 0.006 0.010 0.032 0.000 0.000 863.0 1192.0 1.0
a2[1] 0.021 0.006 0.009 0.032 0.000 0.000 784.0 1103.0 1.0
a2[2] 0.020 0.006 0.010 0.032 0.000 0.000 858.0 992.0 1.0
a2[3] 0.020 0.006 0.010 0.031 0.000 0.000 919.0 1053.0 1.0
a2[4] 0.919 0.012 0.896 0.940 0.000 0.000 1930.0 1290.0 1.0
The posterior mean is 4.69 and 4.80 respectively.
# expected values
a1 = trace.posterior['a1'].mean(axis=(0, 1)).to_numpy()
a2 = trace.posterior['a2'].mean(axis=(0, 1)).to_numpy()
sum(a1 * np.arange(1, 6)), sum(a2 * np.arange(1, 6))
(4.6927501413326596, 4.796011468410374)
The probability of less than 4 stars is 8% and 6% respectively. So the chance of a bad experience is higher in the first restaurant.
# prob of a bad experience, (1 2 or 3)
sum(a1[:3]), sum(a2[:3])
(0.08167586791903829, 0.060920351559323675)
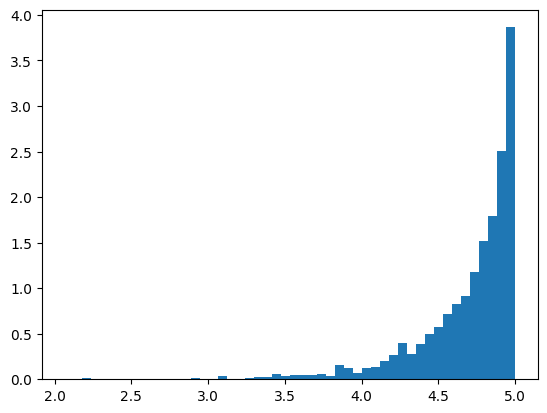
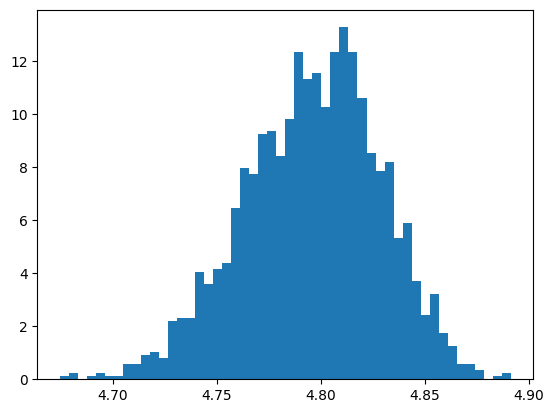
You can see the posterior distribution of the avg stars for the two restaurants. The 90% intervals are (4.00, 4.99) and (4.74, 4.84) respectively. As expected the interval is much smaller for the restaurant with more reviews.
The code can also be found here